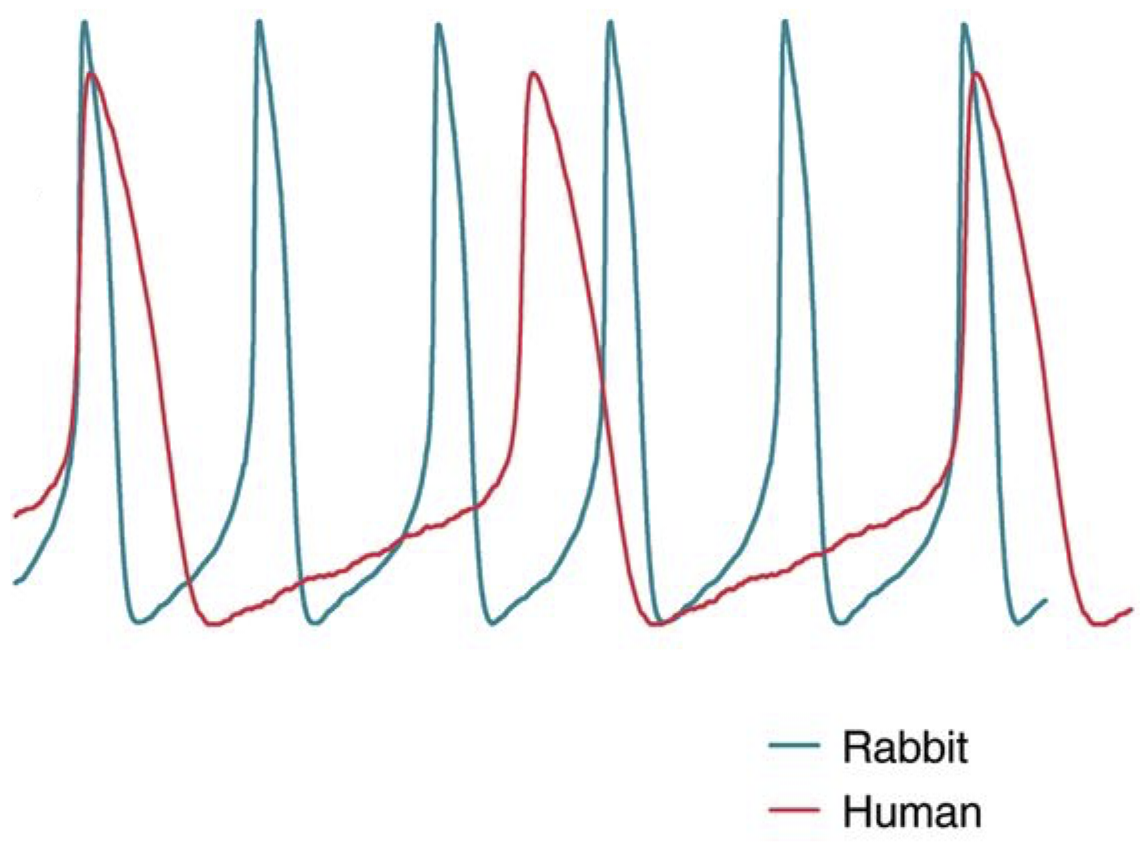
Figure 1 : Battements de cœur chez l'homme et chez le lapin : évolution de l'intensité
À la fin du dix-neuvième siècle, on savait déjà que l’activité cardiaque était associée à la production d’une quantité de courant électrique. On a commencé à quantifier ce courant au début du vingtième siècle (électrocardiogramme). La cellule cardiaque est une cellule polarisée qui a, le long de sa paroi, une série de dipôles, chargés positivement sur la surface externe et négativement sur la surface interne, quand le cœur est au repos (diastole). Quand la cellule est excitée, il y a une chute de la constante diélectrique de la membrane et on a donc des charges négatives qui passent à l’extérieur. Ce phénomène se poursuit jusqu’à la dépolarisation de la cellule, qui atteint alors l’état d’excitation (systole). Après un court délai, des processus physiques et chimiques réparent la cellule et la repolarisent. Le procédé de repolarisation est plus lent que celui de dépolarisation.
Le battement du cœur fait partie des systèmes naturels auto-excités (à partir de n’importe quelle condition initiale, le système approche rapidement un cycle limite stable) pour lesquels on peut remarquer des oscillations avec relaxation. Plusieurs phénomènes présentent ce type d’oscillations : harpe éolienne, marteau pneumatique, grincement d’un couvert sur une assiette, mouvement d’un drapeau dans le vent, tube à néon... et, finalement, le battement du cœur. Ces phénomènes se caractérisent par les propriétés suivantes :
Pour rendre compte de ces propriétés, Van der Pol a proposé de modéliser les battements de cœur comme un circuit RLC, avec une loi d'Ohm non-linéaire. En notant $x$ l'intensité du courant dans l'inductance L et $y$ la tension aux bornes du condensateur C, il obtient le système d'équations différentielles suivant :
$$(S)\ \colon \begin{cases} x'(t) = \varepsilon \left( y(t)-\dfrac{x(t)^{3}}{3}+x(t)\right)\\ y'(t)=-x(t)\vphantom{\left( y(t)-\dfrac{x(t)^{3}}{3}+x(t)\right)} \end{cases},$$où $\varepsilon$ est un paramètre que l'on va choisir pour que le modèle "colle" le plus possible à la réalité.

L'intérêt de bien modéliser l'activité électrique dans le cœur est par exemple de pouvoir configurer les pacemakers de manière à reproduire des battements de la manière la plus naturelle possible.
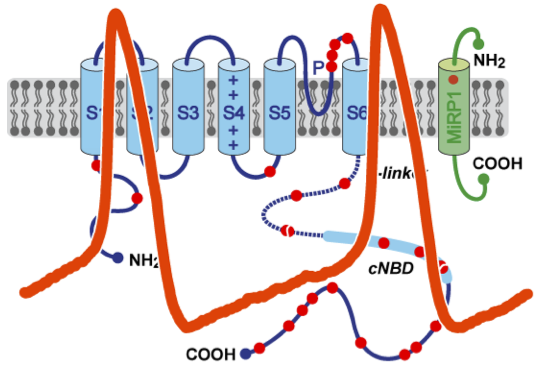
En choisissant $\varepsilon\in ]0,1[$ par exemple, le résultat obtenu est trop proche d'une sinusoïde. On choisira donc $\varepsilon$ assez grand.
Écrire les relations de récurrences obtenues lorsque l'on applique le méthode d'Euler explicite au système $(S)$ afin d'obtenir les approximations $(x_n)$ et $(y_n)$.
Implémenter la méthode d'Euler explicite pour simuler l'évolution de $x$ en fonction de $t$ sur $[0,10]$ pour 3 valeurs différentes de $\varepsilon$. On pourra choisir $x(0)=y(0)=1$.
Obtenir le tracé dans le portrait de phase ($x$ en abscisses, $y$ en ordonnées) pour ces différentes valeurs de $\varepsilon$.
La courbe obtenue est-elle fermée ?
Qu'est-ce que cela signifie sur les fonctions $x$ et $y$ ?
Exprimer le système $(S)$ comme une équation différentielle d'ordre 1 vectorielle.
Coder la méthode d'Euler vectorielle pour simuler à nouveau l'évolution de $x$ en fonction de $t$ avec les mêmes choix de $\varepsilon$ que précédemment.
On étudie l'évolution de la température d'un fil chauffé à une extrémité.
L'étude de l'équation de la chaleur en régime permanent dans un milieu homogène avec source conduit à résoudre l'équation :
$$(\star)\ \colon u^{\prime\prime}(x) + f(x) =0,$$où $u$ désigne la fonction que l'on souhaite déterminer et $f$ est une fonction connue. Les fonctions $u$ et $f$ dépendent uniquement des coordonnées spatiales et non du temps.
On suppose dorénavant que le fil chauffé est de longueur $1$, et que chaque point est repéré par son abscisse $x\in[0,1]$. On fixe un entier $n\geqslant 2$ et on subdivise le segment $[0,1]$ en posant :
$$\forall k\in [\![ 0,n ]\!],\ x_{k}=\frac{k}{n}.$$On pose $h=\frac1n$ le pas de la subdivision et on souhaite déterminer une approximation $y_{k}$ des valeurs $u(x_{k})$.
Pour $k\in [\![ 1,n-1 ]\!]$, on utilise l'approximation suivante :
$$u^{\prime\prime}\left(x_{k}\right)=\frac{u\left(x_{k+1}\right)-2u\left(x_{k}\right)+u\left(x_{k-1}\right)}{h^{2}}. $$Expliquer d'où vient cette approximation.
On impose les conditions au bord suivantes : $y_{0}=y_{1}$ et $y_{n}=0$ (conditions de Neumann et Dirichlet). Elles traduisent des hypothèses physiques sur les extrémités du fil.
$$(\mathcal S)\ \colon \begin{cases} -y_{0}+y_{1}=0\\[5pt] \forall k\in [\![ 1,n-2]\!],\ y_{k-1}-2y_{k}+y_{k+1}=-h^{2}f(x_{k})\\[5pt] y_{n-2}-2y_{n-1}=-h^{2}f(x_{n-1}) \end{cases}$$Justifier que l'on obtient le système $(\mathcal S)$ suivant :
Écrire la matrice (non augmentée) associée au système $(\mathcal S)$.
On admettra que cette matrice est inversible, ce qui implique que le système admet une unique solution.
Dans toute la suite, on fixe la fonction $f\colon x\mapsto 12x(1-x)$.
Écrire une fonction Python
systeme(n)qui construit et renvoie la matrice augmentée associée au système $(\mathcal S)$.
Donner (sans justifier) l'ordre de grandeur (en fonction de $n$) de la complexité de la mise sous forme échelonnée dans l'algorithme du pivot de Gauss (avec recherche partielle de pivot) appliqué à la matrice augmentée associée à $(\mathcal S)$.
Proposer une amélioration de la fonction
transvection(M,i,j,x)tenant compte de la structure particulière de la matrice augmentée associée à $\mathcal (S)$.
Quelle est la nouvelle complexité de la mise sous forme échelonnée dans l'algorithme du pivot de Gauss ainsi modifié ?
On considère une base de données relationnelle de ventes, formée de 5 tables, et dont le schéma est le suivant :
Client (noClient, nom, noTel, adresse)
Article (noArticle, description, prixUnitaire, qteEnStock)
Commande (noCommande, dateCommande, noClient)
LigneCommande (noCommande, noArticle, quantité)
Livraison (noLivraison, dateLiv)
DetailLivraison (noLivraison, noCommande, noArticle, qteLivree)Quel(s) attribut(s) pourrai(en)t servir de clé primaire de la table
LigneCommande?
Formulez les requêtes suivantes en SQL :
- le numéro de commande et la date de commande des commandes du client 42.
les numéros des articles commandés au moins une fois par le client 42 après le 01/04/2021. On rappelle que les dates peuvent être codées sous la forme de chaînes de caractères du type "AAAA-MM-JJ" et qu'elles peuvent alors être comparées à l'aide des opérateurs de comparaison usuels.
Les numéros et noms des clients qui n’ont pas passé de commande au mois de mars de l’année 2021.