Concours blanc 2020 : informatique pour le tennis

Partie I. Présentation générale d'un système d'aide à l'arbitrage

Le système Hawk-eye est un système d’aide à la décision arbitrale utilisé dans le sport de haut niveau, notamment le tennis, un des plus connus. Il a été développé par le Paul Hawkins en 1999 avec pour objectif d’augmenter la qualité des décisions arbitrales et fournir un résultat rapide, clair et précis lors des moments décisifs de rencontres sportives (figure 1). Il a été utilisé pour la première fois au tennis lors du Masters de Miami en 2006. Chaque joueur peut faire appel trois fois par set de cette décision.

Figure 1 : Décision officielle du système Hawk-Eye

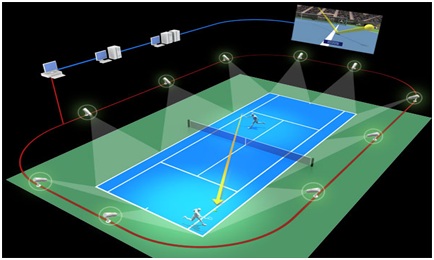
Pour analyser la trajectoire et la position de la balle, le système Hawk-Eye se compose de dix caméras, réparties à égale distance autour du court de tennis dans les tribunes (figure 2). Ces caméras peuvent photographier "en rafale" des objets se déplaçant à une grande vitesse grâce à un capteur photographique. Elles peuvent enregistrer jusqu’à 1 000 images par seconde. Ces images sont ensuite envoyées au poste de commande du système.

Figure 2 : Position des caméras haute vitesse autour du terrain de tennis

L’objectif de l’étude proposée est de réaliser le programme de suivi (tracking) de la trajectoire de la balle de tennis par le système Hawk-eye, la reconstruction de la trajectoire et enfin l’iden- tification de la position de l’impact de la balle avec le sol pour savoir si la balle est dans les limites du terrain ou non. Afin de mieux appréhender le problème, nous commencerons par la modélisation et l’étude théorique de la trajectoire d’une balle de tennis et montrerons en quoi cette seule modélisation est insuffisante pour l’aide à l’arbitrage.

Dans tout le sujet, il sera supposé que les bibliothèques suivantes sont déjà importées comme suit.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

Attention, l’utilisation des fonctions min et max ne sera pas acceptée.

Partie II. Modélisation de la trajectoire de la balle

L’objectif de cette partie est de déterminer la trajectoire théorique d’une balle de tennis et de montrer les limites du résultat obtenu.

La trajectoire d’une balle de tennis dépend de plusieurs paramètres :

• la vitesse de frappe par la raquette du joueur ;
• l’angle de frappe;
• les frottements dans l’air;
• la vitesse de rotation donnée à la balle par la raquette du joueur.

Le schéma de la figure 3 représente un terrain de tennis pour une partie en simple et la trajectoire de la balle dans l’espace de coordonnées $(x,y,z)$. Le repère est choisi de sorte que le plan $(0,\vec x,\vec y)$ soit horizontal.

Figure 3 : Paramétrage du terrain de tennis et trajectoire d’une balle

Paramétrage

• La balle a une masse $m$ et un rayon $R$.
• Le mouvement de la balle est étudié dans le référentiel $\mathscr R$ lié au terrain et supposé galiléen. On lui associe le repère $(O;\vec x,\vec y,\vec z)$, avec $O$ le point de coordonnées $(0,0,0)$.
• La position initiale de la balle est définie dans le référentiel supposé galiléen lié au terrain au point $I$ par $(x_0,y_0,z_0)$.
• La balle est repérée par la position de son centre d’inertie $G$ auquel est associé le vecteur $\vec{OG} = (x+x_0)\vec x + (y+y_0)\vec y + (z+z_0)\vec z$.
• La vitesse de la balle est notée $\vec V = v_x \vec x + v_y \vec y + v_z \vec z$ et sa vitesse initiale $\vec{V_0}$.
• L’angle de frappe entre le plan $(O,\vec x,\vec z)$ et $\vec V$ est $\alpha$ (qui dépend donc de $t$).
• La vitesse de rotation sur elle-même de la balle est notée $\vec \Omega = \Omega \vec z$, où $\Omega$ est supposée constante.
• $\vec g = − g \vec y$ est l’accélération de la pesanteur.

Hypothèses

• On supposera dans toute la suite de cette partie que la balle ne se déplace que dans le plan $(O,\vec x,\vec y)$. Par conséquent, à chaque instant, $v_z = 0$.
• Les différents efforts s’exerçant sur la balle de tennis sont représentés sur la figure 4. $\vec t$ est un vecteur unitaire tangent à la trajectoire et dirigé suivant le sens de la trajectoire. $\vec n$ est un vecteur unitaire normal à la trajectoire.

Figure 4 : Efforts de l’air sur la balle

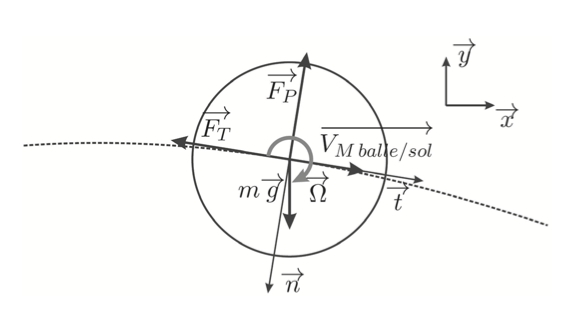
Équations du mouvement de la balle

Le mouvement de la balle de tennis est défini par l’équation suivante :

$$\tag{1} m\dfrac{d^2 \vec{OG}}{dt^2}=m\vec{g}+\vec{F_T}+\vec{F_P}$$

avec $\vec{F_T}=-\dfrac{1}{2}\pi R^2\rho_{\textrm{air}}C_1V^2\vec t$ et $\vec{F_P}=\rho_{\textrm{air}}R^3C_2 V\Omega \vec n$, où $\rho_{\textrm{air}}$ est la masse volumique de l’air (environ $1 \textrm{kg}/\textrm{m}^3$ à température ambiante), $V$ la vitesse de la balle et $C_1$ et $C_2$ deux coefficients sans dimension qui dépendent du nombre de Reynolds.

L’équation $(1)$, une fois projetée dans le plan $ (O,\vec x,\vec y)$, devient :

$$\tag{2} m\dfrac{d^2x(t)}{dt^2}=-\frac{1}{2}\pi R^2 \rho_{\textrm{air}} C_1 V^2\cos(\alpha)-\rho_{\textrm{air}}R^3 C_2 V \Omega \sin(\alpha)$$$$\tag{3} m\dfrac{d^2y(t)}{dt^2}=-mg-\frac{1}{2}\pi R^2 \rho_{\textrm{air}} C_1 V^2\sin(\alpha)+\rho_{\textrm{air}}R^3 C_2 V \Omega \cos(\alpha)$$

On pose $Y=\begin{pmatrix}u\\v\\x\\y\end{pmatrix}$, avec $u(t)=\dfrac{dx(t)}{dt}$ et $v(t)=\dfrac{dy(t)}{dt}$ et dont la condition initiale est $Y_0=\begin{pmatrix}u_0\\v_0\\x_0\\y_0\end{pmatrix}$.

On considérera par la suite que Omega, g, C1, C2, rho_air, R, m ont déjà été définies comme des variables globales que vous pourrez utiliser dans vos scripts et fonctions Python.

Question 1

Exprimer $\cos(\alpha)$, $\sin(\alpha)$ et $V$ en fonction de $u$ et $v$.

Question 2

Mettre les équations $(2)$ et $(3)$ sous la forme d’un système différentiel du type : $\dfrac{dY}{dt}=F(Y)$.

La résolution numérique des équations différentielles (2) et (3) repose sur leur discrétisation temporelle et conduit à déterminer à différents instants $t_i$ une approximation de la solution.

On note $u_i$ et $v_i$ les approximations des composantes du vecteur vitesse $(u(t),v(t))$ et $x_i$ et $y_i$ les approximations des composantes du vecteur position $(x(t), y(t))$ à l’instant $t_i$. On note $h = t_{i+1} − t_i$, le pas de temps, que l'on supposera constant.

Le schéma d’Euler conduit à la relation de récurrence suivante : $$Y_{i+1} =Y_i +h F(Y_i)$$

Question 3

Compléter sur votre copie la fonction euler(T,N,F,Y0) ci-dessous permettant de construire le schéma d’Euler :

def euler (T,N,F,Y0):
    Y=np.zeros((len(Y0),N))
    t=np.arange(0,T,T/N)
    # conditions initiales à compléter
    for i in range(1,N) :
        # zone à compléter
    return t,Y

On remarquera que la taille de Y (qui est un tableau numpy à 2 dimensions) est fixée dès le début de la procédure. On n'utilisera pas de append, mais on construira dans la boucle for les Y[:,i] successifs.

La reconstruction de la trajectoire d’une balle de tennis à partir des lois physiques et des conditions initiales ne se révèle pas satisfaisante en terme de précision pour l’aide à la décision arbitrale. En effet, les paramètres climatiques (vent, pluie, pression atmosphérique...), de déformation de la balle ou tout autre aléa ne sont pas pris en compte a posteriori. Il convient donc d’adopter une autre méthode vérifiant à tout instant la position de la balle ; c’est ce que permet le système Hawk-eye. Nous allons nous intéresser dans la suite à une partie de l’algorithme permettant de vérifier si une balle est bonne et de reconstruire la trajectoire de la balle.

Partie III. Tracking et reconstruction de la trajectoire de la balle de tennis

Comme nous l’avons vu dans la partie présentation et plus particulièrement sur la figure 2, le système Hawk-eye est composé de 10 caméras réparties autour du terrain de tennis. Pour pouvoir obtenir la trajectoire de la balle et déterminer le point d’impact de cette dernière avec le terrain, il est nécessaire de faire appel à une unité de traitement des données de différentes caméras. Cette unité de traitement des données fait appel à un algorithme de calcul qui se décompose en 7 étapes :

• Étape ①; : on détermine les limites du terrain ;
• Étape ② : on réalise le calibrage de la caméra (détermination de sa position, son orientation et ses paramètres intrinsèques) ;
• Étape ③ : on identifie les pixels représentant la balle et on calcule la position 2D dans chaque image de chaque caméra ;
• Étape ④ : on calcule la position 3D de la balle par triangularisation ;
• Étape ⑤ : on assemble les images obtenues ;
• Étape ⑥ : on détermine l’impact de la balle avec le sol sur le terrain ;
• Étape ⑦ : on reconstruit la trajectoire 3D de la balle que l’on affichera pour les spectateurs.

Nous nous proposons dans la suite du sujet de nous intéresser plus spécifiquement aux étapes ③ à ⑦.

III.1 - Détermination de la taille des fichiers récupérés

L’image acquise par la caméra est une image en couleur constituée de trois couches de pixels (RGB, pour Red-Green-Blue). La résolution de l’écran est de $1024$ pixels horizontalement et $768$ verticalement. Les données de l’image sont stockées dans un tableau de type list à trois dimensions : la première dimension correspond à la coordonnée selon $x$, la seconde à la coordonnée selon $y$ et la troisième est une liste de longueur $3$ correspondant à la couleur (rouge, vert ou bleu, indice 0, 1 ou 2).

Ainsi, les dimensions du tableau sont : $n\times m\times 3$ où $n = 1 024$ et $m = 768$. La valeur associée à chaque composante de couleur (R,G,B) d'un pixel est un entier compris entre $0$ et $255$, qui sera codé par un nombre de type uint8 (entier non signé).

Un point joué désigne l’ensemble des coups exécutés par les joueurs, service compris, jusqu’à ce que l’un d’entre eux commette une faute ou un coup gagnant. Un échange désigne un couple de coups joués par les joueurs.

Question 4

On suppose que l’on stocke dans la variable image1 une image enregistrée par la caméra. Indiquer la valeur des expressions suivantes :

• len(image1)
• len(image1[12][244])

Indiquer également le type de l’expression suivante :

• image1[12][244][2]

Question 5

Déterminer, en justifiant succinctement votre calcul, la taille de l’espace mémoire occupé par le tableau représentant l’image émise par la caméra.

Question 6

Estimer un ordre de grandeur de l’espace de stockage à prévoir pour sauvegarder toutes les images des 10 caméras rapides ($1 000$ images/s) correspondant à un point joué, puis à un set. Un set comporte en moyenne $100$ points joués. On pourra estimer à $10$ s la durée moyenne d’un point joué.

Indiquer quel moyen de stockage pourra convenir à la sauvegarde des données.

III.2 - Calcul de la position 2D de la balle (étape ③)

L’objectif de l’algorithme que nous allons étudier ici est d’identifier la position de la balle en prenant en compte sa taille et sa forme sur chaque image enregistrée à l’aide d’une caméra rapide.

L’algorithme doit renvoyer les coordonnées $x$ et $y$ de la balle dans le repère $(O,\vec x ,\vec y ,\vec z )$ et l’instant correspondant $t$ lorsque celle-ci est détectée. Si la balle n’est pas détectée dans le champ de vision de la caméra, l’information retournée sera None. L’algorithme proposé se déroule en plusieurs étapes :

• première étape : détecter tous les objets en mouvement grâce à l’analyse de deux images successives,
• deuxième étape : éliminer les objets en mouvement qui ne peuvent pas correspondre à une balle de tennis selon des critères géométriques,
• troisième étape : éliminer les "balles fausses" détectées en prenant en compte la trajectoire de la balle.

La première étape est réalisée en comparant deux images successives (donc séparées d’un laps de temps très bref). Ces 2 images (image1 et image2) sont quasiment identiques exceptées les zones en mouvement. L’objectif est de créer un nouveau tableau de dimension $n \times m$ (avec $n = 1 024$ et $m = 768$) dans lequel l’élément correspondant à un pixel est un entier compris entre $0$ et $255$. Cet entier correspond à un niveau de gris (le noir correspondant à l’entier $0$ et le blanc à l’entier $255$). Les zones blanches ou claires seront considérées comme des objets en mouvement. Les images sont celles décrites en début de sous-partie III.2 et correspondent à des tableaux à $3$ dimensions de type list : $n \times m \times 3$. Pour détecter les zones en mouvement, l’algorithme propose de calculer pour chaque pixel la somme des différences au carré associées à chaque couleur :

$$\tag{4} \Delta = \sqrt{(r_1 −r_2)^2 +(g_1 −g_2)^2 +(b_1 −b_2)^2}$$

où $r_i$, $g_i$ et $b_i$ représentent respectivement les niveaux de rouge, vert et bleu d’un pixel de coordonnées $(x,y)$ de l’image1 et de l’image2.

En cas de variation importante de couleur, $\Delta$ peut atteindre une valeur supérieure à $255$ ce qui pose des difficultés dans la suite de l’algorithme. On veut garantir $0 \leqslant \Delta \leqslant 255$ et on impose donc la valeur $255$ dans le cas où la formule précédente fournirait une valeur supérieure.

Question 7

Écrire une fonction detection(image1,image2) qui prend en argument 2 images décrites à la sous-partie III.1 et qui renvoie un tableau (de type list de list) de dimension $n \times m$ d’entiers compris entre $0$ et $255$ dans lequel chaque élément correspond à $\Delta$.

Écrire ensuite l’instruction qui permet d’affecter à la variable image_gray le résultat de cette fonction appliquée à deux images im1 et im2.

Le tableau ainsi obtenu est ensuite filtré pour éliminer les pixels trop clairs qui correspondent à des parties figées de l’image. Le seuil doit pouvoir être ajusté pour chaque caméra suivant la luminosité et les conditions météorologiques.

Question 8

Écrire une fonction filtre(image,seuil) qui prend en argument un tableau à deux dimensions (de type list de list) et un flottant et qui renvoie un nouveau tableau de même dimension que celui passé en argument. Chaque élément de ce nouveau tableau prend la valeur $0$ si l’élément correspondant du tableau image est inférieur à la valeur seuil et prend la valeur $1$ sinon.

Nous avons alors obtenu un tableau qui permet de repérer tous les éléments en mouvement dans l’image. Il reste maintenant à détecter les éléments en mouvement qui peuvent être une balle de tennis.

Compte-tenu de la position des caméras latérales et de leur résolution, une balle de tennis occupe au minimum 4 pixels.

Nous allons commencer par éliminer tous les pixels en mouvement qui sont isolés dans le tableau : aucun des pixels adjacents parmi les 8 possibles n’est considéré en mouvement.

Question 9

La fonction filtre_pixel(image) prend en argument un tableau image à deux dimensions, rempli de $0$ et de $1$. Cette fonction doit permettre de balayer tous les éléments du tableau image et de tester s’ils correspondent à un pixel isolé.

Proposer deux schémas permettant d’illustrer le cas d’un pixel isolé et donc à éliminer et celui d’un pixel à conserver.

On considère un pixel de coordonnées $(p,c)$ tel que ce pixel ne soit pas situé sur le bord de l’image. Parmi les 4 tests suivants, choisir celui qui permet de détecter si ce pixel est isolé et, si c’est le cas, de l’éliminer :

Test 1

if image[c-1][p-1]==0 or image[c-1][p+1]==0 or image[c+1][p-1]==0 or image[c+1][p+1] == 0:
    image [ p ] [ c ]=0

Test 2

if image[c-1][p-1]==0 and image[c-1][p+1]==0 and image[c+1][p-1]==0 and image[c+1][p+1] == 0:
    image [ p ] [ c ]=0

Test 3

if image[p][c]==1:
    nb_pixel=-1
    for k in [p-1,p,p+1]:
        for j in [c-1,c,c+1]:
            nb_pixel+=image[k][j]
    if nb_pixel==0:
        image[p][c]=0

Test 4

if image[p][c]==1:
    nb_pixel=-1
    for k in range(p-1,p+1):
        for j in range(c-1,c+1):
            nb_pixel+=image[k][j]
    if nb_pixel==0:
        image[p][c]=0

III.3 - Calcul de la position 3D de la balle par triangularisation (étape ④)

L’objectif de cette sous-partie est de déterminer la position de la balle dans le repère global défini par rapport au terrain à partir de la position de la balle dans deux images de deux caméras différentes.

Une fois que la configuration des caméras a été calibrée, la position de la balle peut être reconstruite dans le repère 3D par stéréo-triangulation. Cela consiste à déterminer la localisation du centre de la balle (noté $M$ de coordonnées $(x, y, z)$ dans le repère global) à partir de la connaissance de la position du centre de la balle dans les images obtenues par deux caméras. La position de la balle dépend de l’espacement e des caméras, également appelé "longueur de la ligne de base stéréo des caméras", de la distance focale $f$ des caméras et de la disparité $d$ qui est la distance entre les centres de la balle dans les images de chaque caméra, ainsi que des coordonnées du centre de la balle dans chacune des images (figure 5).

Figure 5 : Position de la balle à l’instant $i$ dans les images des caméras $1$ et $2$

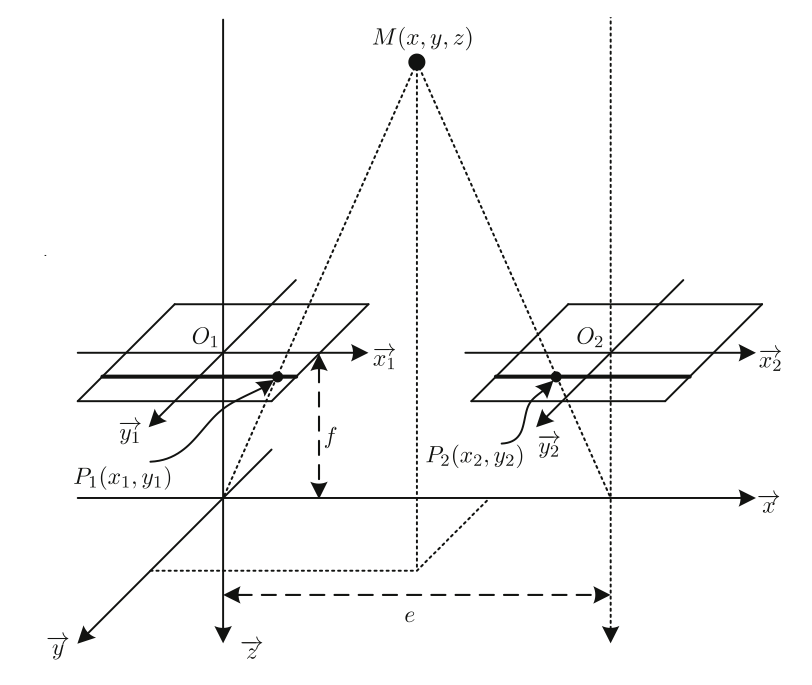
Hypothèses

• On s’intéressera ici à la triangularisation sur deux caméras : les caméras 1 et 2.
• On suppose que la balle est bien détectée par les deux caméras et que les coordonnées relevées correspondent au centre de la balle. Les coordonnées du centre de la balle à l’instant $i$ sont notées respectivement : $P_1$ de coordonnées $(x_1,y_1)$ pour la caméra 1 et $P_2$ de coordonnées $(x_2, y_2)$ pour la caméra 2 dans leurs repères respectifs.
• On suppose que les deux caméras sont disposées à la même hauteur autour du terrain et que leur plan focal est identique.
• On suppose que le temps est bien synchronisé sur les deux caméras.
• On suppose que tous les paramètres de calibration des deux caméras sont connus (matrices intrinsèques et extrinsèques, distance focale, position...).

On calcule les coordonnées du centre de la balle à l’instant $i$ dans le repère de la caméra 1 $(x1i, y1i, z1i)$ grâce aux formules suivantes : $x1i = \frac{e}{d}x_1, y1i = \frac{e}{d}y_1$ et $z1i = \frac{e}{d}f$, avec $d = x_1 − x_2$. Ces coordonnées seront placées par vos soins, si besoin et au bon endroit, dans une liste pos1i=[x1i,y1i,z1i].

Question 10

Écrire une fonction pos_loc(e,f,x1,x2,y1,y2) qui prend en arguments les positions de la balle dans la caméra 1 $(x_1,y_1)$ et la caméra 2 $(x_2,y_2)$ à un instant $i$ puis calcule et renvoie une liste des coordonnées [x1i, y1i, z1i] de la balle dans le repère local de la caméra 1 à un instant $i$.

On calcule ensuite les coordonnées $x$, $y$ et $z$ dans le repère global à l’aide des matrices de passage de la caméra 1 par rapport au repère global. La position et l’orientation de la caméra 1 par rapport au repère global du système sont définies par trois matrices : $T$ sa matrice de translation suivant $\vec x$ , $\vec y$ et $\vec z$ , $R_x$ sa matrice de rotation d’angle $\theta$ suivant $\vec x$ et $R_y$ sa matrice de rotation d’angle $\gamma$ suivant $\vec y$. On obtient la même chose pour la caméra 2 en remplaçant les 1 par des 2. Ces matrices sont supposées connues à chaque instant (résultats de l’étape ② non abordée). La figure 6 illustre la position de la caméra 1 à l’instant $t$.

Figure 6 : Position de la caméra 1 à l’instant $t$$$T_1=\begin{pmatrix}t_{x1}\\t_{y1}\\t_{z1} \end{pmatrix} \qquad R_{x1}=\begin{pmatrix}1&0&0\\0&\cos\theta_1&-\sin\theta1\\0&\sin\theta_1&\cos \theta_1\end{pmatrix} \qquad R_{y1}=\begin{pmatrix}\cos\gamma_1&0&\sin \gamma_1\\0&1&0\\-\sin \gamma_1&0&\cos \gamma_1\end{pmatrix}$$

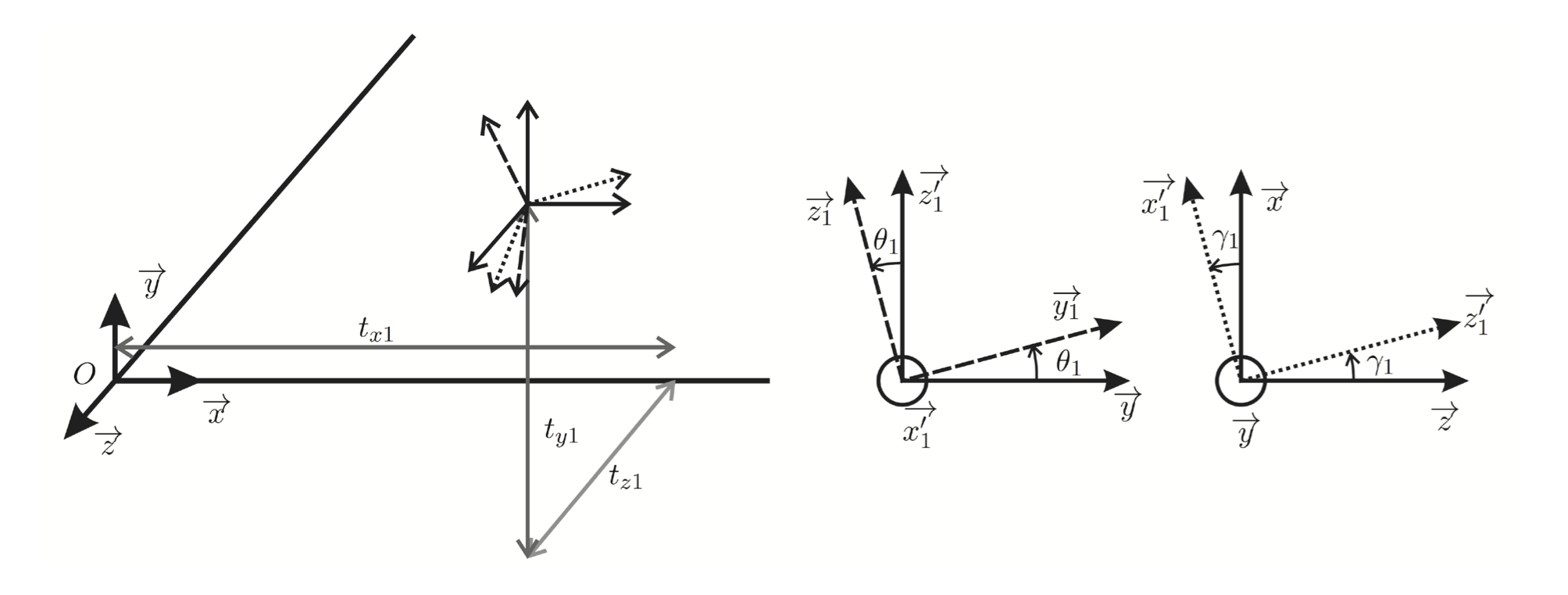
On rappelle que si $R_1$ est la matrice de rotation entre les bases 0 et 1, alors $R_1\times U_1 = U_0$, avec $U_0$ un vecteur défini dans la base 0 et $U_1$ un vecteur défini dans la base 1.

Question 11

Écrire une fonction pos_glo(pos1i,T1,Rx1,Ry1) qui prend en arguments la liste pos1i (résultant de l'applicationde la fonction précédente) et les matrices de translation et rotations T1, Rx1 et Ry1, qui calcule et renvoie une liste des coordonnées de la balle dans le repère global à l’instant $i$ posgi=[xgi,ygi,zgi]. On pourra utiliser les fonctions de numpy pour effectuer les produits matrice-vecteur qui sont rappelées en annexe.

III.4 - Assemblage des positions 3D (étape ⑤)

L’objectif de cette partie est d’assembler les positions 3D de la balle dans le repère global obtenues à l’étape ④.

Les hypothèses sont les mêmes que dans la sous-partie III.3. Les coordonnées locales successives de la balle dans le repère de la caméra 1 sont stockées dans une liste coord_loc=[[x10,y10,z10], [x11,y11,z11],...,[x1i,y1i,z1i],...,[x1N,y1N,z1N]]. La trajectoire complète est obtenue en assemblant les positions successives de la balle dans le repère global.

Question 12

Écrire une fonction traj3D(coord_loc,T1,Rx1,Ry1) qui prend en argument la liste coord_loc et renvoie une liste de l’assemblage dans l’ordre chronologique des $N$ coordonnées de la balle dans le repère global coord_glo=[[xg0,yg0,zg0],[xg1,yg1,zg1],...,[xgN,ygN,zgN]]. On pourra utiliser des fonctions de la sous-partie III.3.

III.5 - Détermination de l’impact de la balle avec le sol sur le terrain (étape ⑥)

L’objectif de cette partie est de déterminer le point d’impact de la balle avec le sol afin de savoir si la balle est restée dans les limites du terrain ou non.

Les hypothèses sont les mêmes que dans la sous-partie III.3.

Cette partie de l’algorithme est primordiale, en effet, c’est à partir du résultat obtenu par cette partie de l’algorithme que l’arbitre rendra sa décision. Le système réel permet de déterminer la forme de l’impact entre la balle et le sol en fonction de la déformation de la balle. Afin de faciliter la résolution du problème, la déformation de la balle ne sera pas prise en compte.

Hypothèses

• On suppose que la balle est indéformable (et donc que le point d’impact est ponctuel) et de rayon $R=0,033$ m.
• La position du terrain (et donc les lignes) est parfaitement connue dans le repère global.
• On considère dans notre cas que le point étudié se fait durant l’échange de balle entre les joueurs et non sur un service.
• On suppose que le terrain est parfaitement plat.

Les coordonnées du point d’impact de la balle avec le sol sont déterminées de la manière suivante : on vient détecter quand la coordonnée suivant $y$ est égale à $R$ et on relève les positions correspondantes suivant $x$ et $z$.

Si la position $y$ comprise entre $R$ et $R+\varepsilon$ ne se trouve dans aucune image, on détermine les coordonnées moyennes suivant $x$ et $z$ des deux images encadrant le moment où il y a eu inversion du sens de déplacement de la balle selon $y$ (descente, puis remontée). La donnée $\varepsilon$ sera notée eps dans le programme.

Question 13

Écrire une fonction det_impact(coord_glo,eps) qui prend en argument la liste coord_glo et le flottant eps puis calcule et renvoie la position de l’impact de la balle dans le repère global : une liste de listes impact=[x_imp,z_imp].

Le terrain comme présenté sur la figure 3 fait $L = 24$ m de long sur $l = 11$ m de large. On considère que le point origine du repère global est le point $O$.

Question 14

Écrire une fonction res_final(impact,L,l) qui prend en argument la liste impact, les dimensions du terrain L et l et qui renvoie True si l’impact de la balle a eu lieu dans les limites du terrain et False sinon.

III.6 - Reconstruction de la trajectoire 3D de la balle (étape ⑦)

L’objectif de cette sous-partie est d’afficher la trajectoire 3D de la balle reconstruite à l’étape ⑤ pour que les spectateurs puissent la visualiser.

Question 15

À partir de la documentation sur le tracé 3D en Python, fournie en annexe, écrire une fonction vis_traj3D(coord_glo) qui prend en argument la liste (de listes) coord_glo et permet d’afficher la trajectoire 3D de la balle.

Partie IV. Exploitation des données fournies par le Hawk-eye

L’objectif de cette partie est de montrer comment utiliser les informations fournies par le système Hawk-eye à des fins d’entraînement ou de visualisation à la télévision.

Le système Hawk-eye est une mine d’informations pour analyser les statistiques des matchs de tennis. Les données sont ainsi utilisées par les chaînes de télévisions lors des retransmissions des matchs mais également par les entraîneurs après les matchs en vue d’adapter leurs programmes d’entraînement.

Ces données d’un tournoi sont stockées dans une base de données constituée de deux tables. La table MATCHS contient les différents matchs d’un tournoi avec les attributs :

• id : identifiant (de type entier), clé primaire ;
• tournoi : nom du tournoi (de type texte) ;
• numero : numéro du match dans la planification du tournoi ; il s'agit d'entiers numérotés à partir de $1$ et par ordre de planification croissant (la finale d'un tournoi est donc le plus grand numéro possible associé à ce tournoi)
• date : date à laquelle le match s’est déroulé ;
• joueur1 : nom du premier joueur ;
• joueur2 : nom du deuxième joueur (les joueurs 1 et 2 sont rangés par ordre alphabétique) ;
• autres attributs non détaillés...

La table POINTS contient des entités correspondant aux points joués lors d’un match. Elle contient les attributs :

• id : identifiant (de type entier), clé primaire ;
• mid : identifiant du match (de type entier), clé étrangère pointant vers l'attribut id de la table MATCHS;
• echange : nombre d’échanges (de type entier) ;
• fichier : nom du fichier image de la trajectoire (stockée) correspondant au point ;
• autres attributs non détaillés...

Question 16

Rappeler la définition et l’intérêt d’une clé primaire.

Question 17

Écrire une requête SQL permettant d’afficher les identifiants des matchs joués par Federer.

Question 18

Écrire une requête SQL permettant d’afficher le nombre d’échanges maximum lors du match dont l’identifiant est mid=4.

Question 19

Écrire une requête SQL permettant de récupérer le nom des fichiers de toutes les images qui correspondent au match numéro 127 du tournoi "AO17M".

Question 20

Écrire une requête SQL permettant de récupérer le nombre d'échanges maximum joué par point pour chaque tournoi répertorié dans la base de données. On classera les résultats par ordre décroissant d'échanges joués.

Question 21 (hors barême)

Le système hawk-eye a été utilisé sur la balle de match lors d'une finale de Grand Chelem opposant Federer à Nadal, scellant la victoire du Maestro suisse. De quel tournoi et de quelle année s'agissait-il ?